目錄

• • 1、STN的作用
  • • • 1.1 靈感來源
      • 1.2 什么是STN？
  • 2、STN網絡架構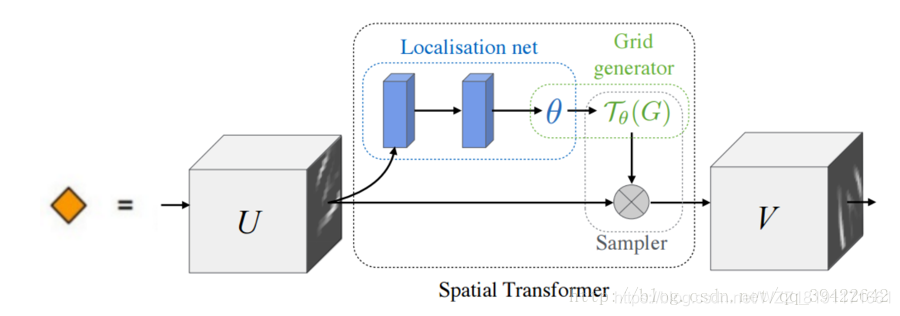
  • 3、Localisation net是如何實現參數的選取的？
  • • • 3.1 如何實現平移變換
      • 3.2 如何實現縮放變換
      • 3.3 如何實現旋轉變換
      • 3.4 如何實現裁剪變換
      • 3.5 總結
  • 4、Grid generator如何實現像素點坐標的對應關系？
  • • • 4.1 為什么會有坐標的問題？
      • 4.2 仿射變換關系
  • 5、Sampler實現坐標求解的可微性
  • • • 5.1 小數坐標問題的提出
      • 5.2 解決輸出坐標為小數的問題
      • 5.3 Sampler的數學原理
  • 6、Spatial Transformer Networks（STN)
  • 7、STN 代碼實現
  • 參考資料
  • 注意事項

1、STN的作用

1.1 靈感來源

??普通的CNN能夠顯示的學習平移不變性，以及隱式的學習旋轉不變性，但attention model 告訴我們，與其讓網絡隱式的學習到某種能力，不如為網絡設計一個顯式的處理模塊，專門處理以上的各種變換。因此，DeepMind就設計了Spatial Transformer Layer，簡稱STL來完成這樣的功能。

1.2 什么是STN？

??關于平移不變性 ，對于CNN來說，如果移動一張圖片中的物體，那應該是不太一樣的。假設物體在圖像的左上角，我們做卷積，采樣都不會改變特征的位置，糟糕的事情在我們把特征平滑后后接入了全連接層，而全連接層本身并不具備 平移不變性 的特征。但是 CNN 有一個采樣層，假設某個物體移動了很小的范圍，經過采樣后，它的輸出可能和沒有移動的時候是一樣的，這是 CNN 可以有小范圍的平移不變性 的原因。

??如上圖所示，如果是手寫數字識別，圖中只有一小塊是數字，其他大部分地區都是黑色的，或者是小噪音。假如要識別，用Transformer Layer層來對圖片數據進行旋轉縮放，只取其中的一部分，放到之后然后經過CNN就能識別了。我們發現，它其實也是一個layer，放在了CNN的前面，用來轉換輸入的圖片數據，其實也可以轉換feature map,因為feature map說白了就是濃縮的圖片數據，所以Transformer layer也可以放到CNN里面。

2、STN網絡架構

??上圖是Spatial Transformer Networks的網絡結構，它主要由3部分組成，它們的功能和名稱如下：參數預測：Localisation net、坐標映射：Grid generator、像素的采集：Sampler。

??上圖展示了一個平移變換的過程，也就是STN所做的事情。假設左邊是Layer l?1的輸出，也就是STN的輸入，最右邊為變換后的結果。假設是一個全連接層，n,m代表輸出的值在輸出矩陣中的下標，輸入的值通過權值w，做一個組合，完成這樣的變換。
??假如要生成$a_{11}^l$,那就是將左邊矩陣的九個輸入元素，全部乘以一個權值，加權相加：$a_{11}^l=w_{1111}^l{a}_{11}^{l?1}+w_{1112}^l{a}_{12}^{l?1}+w_{1113}^l{a}_{13}^{l?1}+?+w_{1133}^l{a}_{33}^{l?1}$。這僅僅是$a_{11}^l$的值，其他的結果也是這樣算出來的，具體的計算公式如下所示：$$a_{nm}^l=\sum _{i=1}^3\sum _{j=1}^3{w}_{nm,ij}^l{a}_{ij}^{l?1}$$通過調整這些權值，就可以達到縮放和平移的目的，其實這就是變換的基本思路。在整個的變換過程中，會涉及到3個關鍵的問題需要去解決，具體的問題如下所示：

• 問題1-應該如何確定這些參數？
• 問題2-圖片的像素點可以當成坐標，在平移過程中怎么實現原圖片與平移后圖片的坐標映射關系？
• 問題3-參數調整過程中，權值一定不可能都是整數，那輸出的坐標有可能是小數，但實際坐標都是整數的，如果實現小數與整數之間的連接？

3、Localisation net是如何實現參數的選取的？

3.1 如何實現平移變換

??對于平移變換而言，比如從$a_{11}^{l?1}$平移到$a_{21}^l$，得到的$a_{21}^l$可以使用下式來表示：$$a_{21}^l=w_{2111}^l{a}_{11}^{l?1}+w_{2112}^l{a}_{12}^{l?1}+w_{2113}^l{a}_{13}^{l?1}+?+w_{2133}^l{a}_{33}^{l?1}$$，當$w_{2111}^l=1$，其余均為0時，上式則可以簡化為：$$a_{21}^l=1?a_{11}^{l_{1}1}$$，這樣就完成了整個平移變換，其它的平移也可以使用類似的方法來獲得。

3.2 如何實現縮放變換

??如果想要放大一張圖片，只需要在X軸和Y軸方向上同時X2就可以啦，這樣就可以達到放大的效果。上述過程可以用下圖中的矩陣表達式來表示。縮小圖片的原理和放大圖片的原理很相似，具體的實現細節請看下圖。

3.3 如何實現旋轉變換

??一個圓圈的角度是360度，我們可以通過控制水平和豎直兩個方向來實現旋轉。

由點A旋轉θ度角，到達點B.得到下式：$$\begin{array}{l}{x}^{\prime }=R\cos \alpha \\ y^{\prime }=R\sin \alpha \end{array}$$ 由A點可得下式：$$\begin{array}{l}x=R\cos (\alpha +\theta )\\ y=R\sin (\alpha +\theta )\end{array}$$ 將上式展開可得：$$\begin{array}{l}x=R\cos \alpha \cos \theta ?R\sin \alpha \sin \theta \\ y=R\sin \alpha \cos \theta +R\cos \alpha \sin \theta \end{array}$$ 把未知數α替換掉可得下式：$$\begin{array}{rl}x& =x^{\prime }\cos \theta ?y^{\prime }\sin \theta \\ y& =y^{\prime }\cos \theta +x^{\prime }\sin \theta \end{array}$$ 總而言之，我們可以簡單的理解為cosθ,sinθ就是控制這樣的方向的，把它當成權值參數，寫成矩陣形式，就完成了旋轉操作。

3.4 如何實現裁剪變換

??剪切變換相當于將圖片沿x和y兩個方向拉伸，且x方向拉伸長度與y有關，y方向拉伸長度與x有關，用矩陣形式表示前切變換如下：

3.5 總結

??通過上面的分析，我們發現所有的這些操作，只需要六個參數[2X3]就可以實現各種變換功能啦，所以我們可以把feature map U作為輸入，過連續若干層計算（如卷積、FC等），回歸出參數θ，在我們的例子中就是一個[2，3]大小的6維仿射變換參數，用于下一步計算。

4、Grid generator如何實現像素點坐標的對應關系？

4.1 為什么會有坐標的問題？

??由上面的公式，我們可以發現，無論如何做旋轉，縮放，平移，只用到六個參數就可以了，具體如下圖所示：

??縮放的本質，其實就是在原樣本上面進行采樣，獲得對應的像素點，通俗點說，就是輸出的圖片(i,j)的位置上，要對應輸入圖片的哪個位置？

??如圖所示旋轉縮放操作，我們把像素點看成是坐標中的一個小方格，輸入的圖片$U\in R^{HxWxC}$可以是一張圖片，或者feature map，其中H表示高，W表示寬，C表示顏色通道。經過變換$T_{\theta }(G)$,θ是上一個部分（Localisation net）生成的參數，生成了圖片$V\in R^{H^{\prime }x{W}^{\prime }xC}$,它的像素相當于被貼在了圖片的固定位置上，用$G=G_i$表示，像素點的位置可以表示為$G_i=\left\{x_i^t,y_i^t\right\}$,這就是我們在這一階段要確定的坐標。

4.2 仿射變換關系

??上圖展示的是一個坐標轉換變換關系：其中$\left(x_i^t,y_i^t\right)$表示的是輸出目標圖片的坐標，$\left(x_i^s,y_i^s\right)$表示原圖片的坐標，$A_{\theta }$表示仿射關系。我們的仿射變換關系是：從目標圖片------->原圖片。作者在論文中寫的比較模糊，比較滿意的解釋是坐標映射的作用，其實是讓目標圖片在原圖片上采樣，每次從原圖片的不同坐標上采集像素到目標圖片上，而且要把目標圖片貼滿，每次目標圖片的坐標都要遍歷一遍，是固定的，而采集的原圖片的坐標是不固定的，因此用這樣的映射。

??如圖所示，假設只有平移變換，這個過程就相當于一個拼圖的過程，左圖是一些像素點，右圖是我們的目標，我們的目標是確定的，目標圖的方框是確定的，圖像也是確定的，這就是我們的目標，我們要從左邊的小方塊中拿一個小方塊放在右邊的空白方框上，因為一開始右邊的方框是沒有圖的，只有坐標，為了確定拿過來的這個小方塊應該放在哪里，我們需要遍歷一遍右邊這個方框的坐標，然后再決定應該放在哪個位置。所以每次從左邊拿過來的方塊是不固定的，而右邊待填充的方框卻是固定的，所以定義從目標圖片------->原圖片的坐標映射關系更加合理，且方便。

5、Sampler實現坐標求解的可微性

5.1 小數坐標問題的提出

??我們可以假設一下我們的權值矩陣的參數是如下這幾個數，x,y分別表示的是他們的下標，經過變換后，可以得到如下的變換關系。

前面舉的例子中，權值都是整數，計算的結果也必定是整數，如果不是整數呢？

假如權值是小數，那得到的值也一定是小數，1.6,2.4，但是沒有元素的下標索引是小數呀。那不然取最近吧，那就得到2，2了，也就是與$a_{22}^l$對應了。

5.2 解決輸出坐標為小數的問題

??使用上面的四舍五入顯然是不能進行梯度下降來回傳梯度的。由于梯度下降是一步一步調整的，而且調整的數值都比較小，哪怕權值參數有小范圍的變化，雖然最后的輸出也會有小范圍的變化，比如一步迭代后，結果有：1.6→1.64,2.4→2.38。但是即使有這樣的改變，結果依然是$a_{22}^{l_1}\to a_{22}^l$的對應關系沒有一點變化，所以output依然沒有變，我們沒有辦法微分了，也就是梯度依然為0呀，梯度為0就沒有可學習的空間呀。所以我們需要做一個小小的調整。
??仔細思考一下這個問題是什么造成的，我們發現其實在推導SVM的時候，我們也遇到過相同的問題，當時我們如果只是記錄那些出界的點的個數，好像也是不能求梯度的，當時我們是用了hing loss，來計算一下出界點到邊界的距離，來優化那個距離的，我們這里也類似，我們可以計算一下到輸出[1.6,2.4]附近的主要元素，如下所示，計算一下輸出的結果與他們的下標的距離，可得：

然后做如下更改：

他們對應的權值都是與結果對應的距離相關的，如果目標圖片發生了小范圍的變化，這個式子也是可以捕捉到這樣的變化的，這樣就能用梯度下降法來優化了。

5.3 Sampler的數學原理

??論文作者對我們前面的過程給出了非常嚴密的證明過程，以下是我對論文的轉述。每次變換，相當于從原圖片$\left(x_i^s,y_i^s\right)$中，經過仿射變換，確定目標圖片的像素點坐標$\left(x_i^t,y_i^t\right)$的過程,這個過程可以用公式表示為：

kernel k表示一種線性插值方法，比如雙線性插值，更詳細的請參考該鏈接，${?}_x,{?}_y$表示插值函數的參數；$U_{nm}^c$表示位于顏色通道C中坐標為(n,m)的值。
如果使用雙線性插值，則可以使用下式來表示：

為了允許反向傳播回傳損失，我們可以求對該函數求偏導：

對于$y_i^s$的偏導也類似，如果就能實現這一步的梯度計算，而對于$=\frac{?x_i^s}{?\theta },\frac{?y_i^s}{?\theta }$的求解也很簡單，所以整個過程按照Localisation net←Grid generator←Sampler的梯度回傳就能走通了。

6、Spatial Transformer Networks（STN)

??將這三個組塊結合起來，就構成了完整STN網絡結構了。這個網絡可以加入到CNN的任意位置，而且相應的計算量也很少。將 spatial transformers 模塊集成到 cnn 網絡中，允許網絡自動地學習如何進行 feature_map 的轉變，從而有助于降低網絡訓練中整體的代價。定位網絡中輸出的值，指明了如何對每個訓練數據進行轉化。

7、STN 代碼實現

STN結構示例如下所示：

class STN(nn.HybridBlock):##繼承HybridBlock模塊，可以方便的hybrid，將命令式編程轉換為符號式提升性能但損失了一定的靈活性def __init__(self):super(STN, self).__init__()with self.name_scope():# 使用name_scope可以自動給每一層生成獨一無二的名字方便讀取特定層# Spatial transformer localization-network# loc 定義了兩層卷積網絡loc = self.localization = nn.HybridSequential() loc.add(nn.Conv2D(8, kernel_size=7))loc.add(nn.MaxPool2D(strides=2))loc.add(nn.Activation(activation='relu'))loc.add(nn.Conv2D(10, kernel_size=5))loc.add(nn.MaxPool2D(strides=2))loc.add(nn.Activation(activation='relu'))# 采用兩層全連接層，回歸出仿射變換所需的參數θ（6，） # Regressor for the 3 * 2 affine matrixfc_loc = self.fc_loc = nn.HybridSequential()fc_loc.add(nn.Dense(32,activation='relu'))# 將該層w初始化為全零，b初始化為[1,0,0,0,1,0]fc_loc.add(nn.Dense(3 * 2,weight_initializer='zeros'))# Spatial transformer network forward function# 使用hybrid_forward需要增加F參數，它會自動判定前向過程中調用nd還是sym def hybrid_forward(self,F, x): xs = self.localization(x)xs = xs.reshape((-1, 10 * 3 * 3))theta = self.fc_loc(xs)theta = theta.reshape((-1, 2*3))# MxNet 已經定義好了相應的產生網格和采樣的函數接口grid = F.GridGenerator(data=theta, transform_type='affine',target_shape=(28,28),name='grid')x = F.BilinearSampler(data=x,grid=grid,name='sampler' )return x

主體網絡代碼如下所示：

class Net(nn.HybridBlock):def __init__(self):super(Net, self).__init__()# 對輸入圖片進行STN變換后送入一個簡單的兩層卷積，兩層全連接網絡with self.name_scope():self.model = nn.HybridSequential()self.model.add(STN())self.model.add(nn.Conv2D(10, kernel_size=5))self.model.add(nn.MaxPool2D())self.model.add(nn.Activation(activation='relu'))self.model.add(nn.Conv2D(20, kernel_size=5))self.model.add(nn.Dropout(.5))self.model.add(nn.MaxPool2D())self.model.add(nn.Activation(activation='relu'))self.model.add(nn.Flatten())self.model.add(nn.Dense(50))self.model.add(nn.Activation(activation='relu'))self.model.add(nn.Dropout(.5))self.model.add(nn.Dense(10))def hybrid_forward(self,F, x):for i,b in enumerate(self.model):x = b(x)return x

參考資料

[1] STN論文
[2] 參考博客1
[3] 參考博客2

注意事項

[1] 該博客轉載自該博客；
[2] 由于個人能力有限，該博客可能存在很多的問題，希望大家能夠提出改進意見。
[3] 如果您在閱讀本博客時遇到不理解的地方，希望您可以聯系我，我會及時的回復您，和您交流想法和意見，謝謝。
[4] 本人業余時間承接各種本科畢設設計和各種小項目，包括圖像處理（數據挖掘、機器學習、深度學習等）、matlab仿真、python算法及仿真等，有需要的請加QQ：1575262785詳聊，備注“項目”！！！

總結

以上是生活随笔為你收集整理的Spatial Transformer Networks（STN）详解的全部內容，希望文章能夠幫你解決所遇到的問題。

如果覺得生活随笔網站內容還不錯，歡迎將生活随笔推薦給好友。