版權(quán)聲明：本文為博主原創(chuàng)文章，未經(jīng)博主允許不得轉(zhuǎn)載。

Pythagoras theorem（勾股定理）

一個直角三角形中，兩個直角邊邊長的平方加起來等于斜邊長的平方。 如果設(shè)直角三角形的兩條直角邊長度分別是a和b，斜邊長度是c，那么可以用數(shù)學(xué)語言表達：

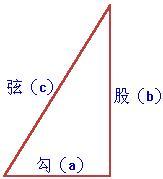 a2+b2=c2 滿足這個等式且沒有公因數(shù)的的三元數(shù)組（a,b,c）稱為勾股數(shù)。 可證a、b兩個數(shù)必然一奇一偶，證明如下： 如果數(shù)a,b都是奇數(shù)，則數(shù)c必為偶數(shù)。可設(shè)a=2x+1,b=2y+1,c=2z,有 (2x+1)2+(2y+1)2=(2z)2 展開化簡得到下式： 2x2+2x+2y2+2y+1=2z2 上式左邊為奇數(shù)，右邊為偶數(shù)，等式顯然不成立； 如果數(shù)a，b都是偶數(shù)，意味著c也是偶數(shù)。此時a,b,c都可以被2整除，此時a,b,c不互質(zhì)。 證畢。 ———-

定理

由a2+b2=c2可得a2=(c?b)(c+b)
??假設(shè)存在一個數(shù)d是(c-b),(c+b)的公因數(shù)，即d可以整除(c-b)和(c+b)，則d也可以整除

（c+b）+（c-b）= 2c 與 （c+b）-（c-b）= 2b

??故d整除2b和2c.而b、c沒有公因數(shù)，因為我們假設(shè)（a,b,c）為本原勾股數(shù)組，可以得出d一定是1或2。但d也整除(c+b)(c?b)=a2 且a為奇數(shù)，所以d只能為1，所以(c-b),(c+b)沒有公因數(shù)。
?? 現(xiàn)在我們知道c-b與c+b沒有公因數(shù)且a2=(c?b)(c+b) ,所以c-b,c+b的積是平方數(shù)，當(dāng)且僅當(dāng)c-b和c+b本身都是平方數(shù)。記

c+b=s2 , c?b=t2
其中s>t?1 為沒有公因數(shù)的奇數(shù)。關(guān)于b和c解方程組得

c=s2+t22 , b=s2?t22

于是???????????????????? a=(c+b)(c?b)???????????√=st

所以有以下定理

Pythagorean Triples  Theorem：We will get every primitive Pythagorean triple(a,b,c) with a odd and b even by using the formulas:

a=st， b=s2?t22， c=s2+t22(s>t?1)

通過這個公式，取不同s，t的值便可生成不同的勾股數(shù)。

下表為s?9 的所有勾股數(shù)

sta=stb=s2?t22c=s2+t22

3	1	3	4	5
5	1	5	12	13
7	1	7	24	25
9	1	9	40	41
5	3	15	8	17
7	3	21	20	29
7	5	35	12	37
9	5	45	28	53
9	7	63	16	65

---

轉(zhuǎn)載于:https://www.cnblogs.com/vocaloid-fan1995/p/10363838.html

總結(jié)

以上是生活随笔為你收集整理的数论概论学习笔记（一）——勾股数的全部內(nèi)容，希望文章能夠幫你解決所遇到的問題。

如果覺得生活随笔網(wǎng)站內(nèi)容還不錯，歡迎將生活随笔推薦給好友。