作者 | JNK789? ?編譯 | Flin??來源 | analyticsvidhya

我們正在使用 Jupyter notebook 來運行我們的代碼。我們建議在Google Colaboratory上遵循本教程。你可以查看此鏈接以獲取有關其用法的更多信息。

• https://www.analyticsvidhya.com/blog/2020/03/google-colab-machine-learning-deep-learning/

為了完成本教程，假設你已具備 PyTorch 和 Python 編程的先驗知識。不需要機器學習的先決知識。你可以查看我們之前關于 PyTorch 的博客以熟悉它。

• https://www.analyticsvidhya.com/blog/2021/04/a-gentle-introduction-to-pytorch-library/

線性回歸簡介

反向傳播是深度學習中一種強大的技術，用于更新權重和偏差，從而使模型能夠學習。為了更好地說明反向傳播，讓我們看一下線性回歸模型在 PyTorch 中的實現

線性回歸是機器學習中的基本算法之一。線性回歸在輸入特征 (X) 和輸出標簽 (y) 之間建立線性關系。

在線性回歸中，每個輸出標簽都表示為使用權重和偏差的輸入特征的線性函數。這些權重和偏差是隨機初始化的模型參數，然后通過數據集的每個訓練/學習周期進行更新。在經過一次訓練數據迭代后訓練模型和更新參數被稱為一個時期。

所以現在我們應該訓練模型幾個時期，以便權重和偏差可以學習輸入特征和輸出標簽之間的線性關系。

因此，在本教程中，讓我們創建一個假設數據模型，該模型由芒果和橙子的作物產量組成，并給出了特定地點的平均溫度、年降雨量和濕度。訓練數據如下：

地區溫度（華氏度）降雨量（毫米）濕度 （％）芒果（噸）橙子（噸）

A	73	67	43	56	70
B	91	88	64	81	101
C	87	134	58	119	133
D	102	43	37	22	37
E	69	96	70	103	119
F	74	66	43	57	69
G	91	87	65	80	102
H	88	134	59	118	132
I	101	44	37	21	38
J	68	96	71	104	118
鉀	73	66	44	57	69
升	92	87	64	82	100
米	87	135	57	118	134
N	103	43	36	20	38
哦	68	97	70	102	120

在線性回歸中，每個目標標簽都表示為輸入變量的加權總和以及偏差，即

芒果 = w₁₁ * 溫度 + w ₁₂ * 降雨量 + w ₁₃ * 濕度 + b ₁

橙子 = w ₂₁ * 溫度 + w ₂₂ * 降雨量 + w 23 * 濕度 + b ₂

最初，權重和偏差是隨機初始化的，然后在訓練過程中進行相應的更新，以便這些權重和偏差能夠預測任何地區的芒果和橙子產量，前提是溫度、降雨量和濕度達到一定的準確度。

簡而言之，這就是機器學習。

所以現在讓我們開始使用 Pytorch 實現

進口

導入所需的庫

import?torch import?numpy?as?np

加載數據

上表中給出的訓練數據可以使用 NumPy 表示為矩陣。所以讓我們分別定義輸入和目標，

inputs?=?np.array([[73,?67,?43],?[91,?88,?64],?[87,?134,?58],?[102,?43,?37],?[69,?96,?70],?[74,?66,?43],?[91,?87,?65],?[88,?134,?59],?[101,?44,?37],?[68,?96,?71],?[73,?66,?44],?[92,?87,?64],?[87,?135,?57],?[103,?43,?36],?[68,?97,?70]],?dtype='float32') targets?=?np.array([[56,?70],?[81,?101],?[119,?133],?[22,?37],?[103,?119],[57,?69],?[80,?102],?[118,?132],?[21,?38],?[104,?118],?[57,?69],?[82,?100],?[118,?134],?[20,?38],?[102,?120]],?dtype='float32')

輸入矩陣和目標矩陣都作為 NumPy 數組加載。

這應該使用torch.from_numpy()方法轉換為torch張量 ，

inputs?=?torch.from_numpy(inputs) targets?=?torch.from_numpy(targets)

我們可以檢查兩個張量，

print(inputs)

輸出：


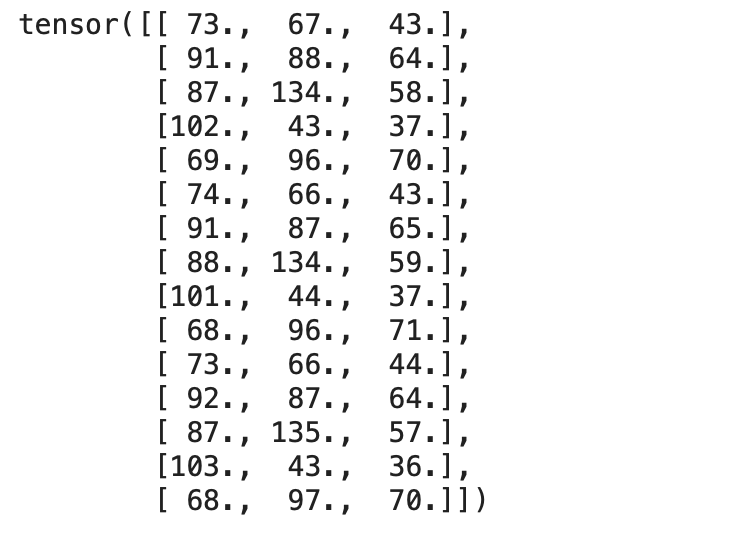
print(targets)

輸出：


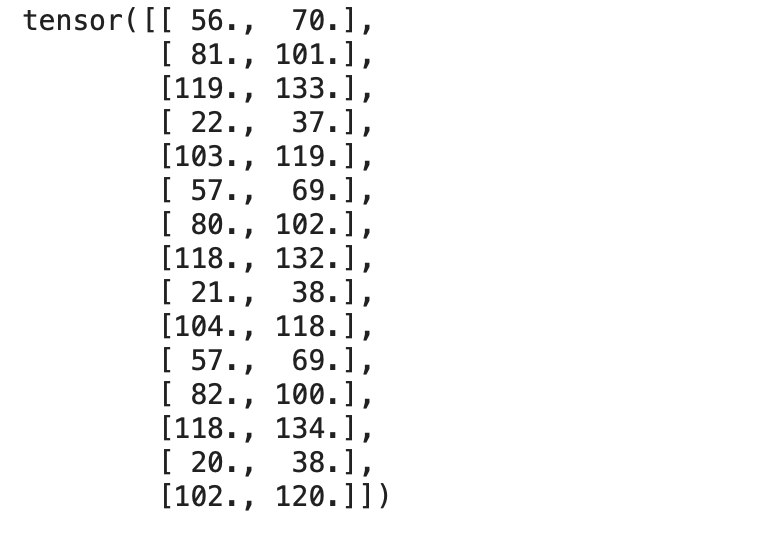
現在讓我們創建一個TensorDataset，它將輸入和目標張量包裝到一個數據集中。讓我們從torch.utils.data導入TensorDataset方法。

我們可以以元組的形式訪問數據集中的行。

from?torch.utils.data?import?TensorDataset dataset?=?TensorDataset(inputs,?targets)

我們可以使用 Python 中的索引從定義的數據集中訪問輸入行和相應的目標。

dataset[:3]


現在讓我們將數據集轉換為數據加載器，它可以在訓練期間將數據拆分為預定義批量大小的批次。

使用 Pytorch 的DataLoader類，我們可以將數據集轉換為預定義批量大小的批次，并通過從數據集中隨機挑選樣本來創建批次。

from?torch.utils.data?import?DataLoaderbatch_size?=?3 train_loader?=?DataLoader(dataset,?batch_size=batch_size,?shuffle=True)

我們可以使用 for 循環將DataLoader 中的數據作為包含輸入和相應目標的元組對訪問，這使我們能夠將批次直接加載到訓練循環中。

#?A?Batch?Sample for?inp,target?in?train_loader:print(inp)print(target)break

輸出：


現在我們的數據已準備好進行訓練，讓我們定義線性回歸算法。

線性回歸——從頭開始

在統計建模中，回歸分析是一組統計過程，用于估計因變量與一個或多個自變量之間的關系。-維基百科

讓我們從頭開始實現一個線性回歸模型。我們應該找到上述方程中指定的最佳權重和偏差，以便它定義輸入和輸出之間的理想線性關系。

因此，我們定義了一組權重，如上述等式，以建立與輸入特征和目標的線性關系。在這里，我們還將超參數（即權重和偏差）的requires_grad屬性設置 為True。

w?=?torch.randn(2,?3,?requires_grad=True) b?=?torch.randn(2,?requires_grad=True) print(w) print(b)

輸出：


torch.randn從均值 0 和標準差 1 的均勻分布中隨機生成張量。

線性回歸方程為 y = w * X + b，其中

• y是輸出或因變量

• X是輸入或自變量

• w & b分別是權重和偏差

因此，現在讓我們定義我們的線性回歸模型，

def?model(X):return?X?@?w.t()?+?b

該模型只是一個建立權重和輸出之間線性關系的數學方程。

使用輸入批次和權重的轉置執行矩陣乘法（@ 表示矩陣乘法）。

現在讓我們為一批數據預測模型的輸出，

for?x,y?in?train_loader:preds?=?model(x)print("Prediction?is?:n",preds)print("nActual?targets?is?:n",y)break

輸出：


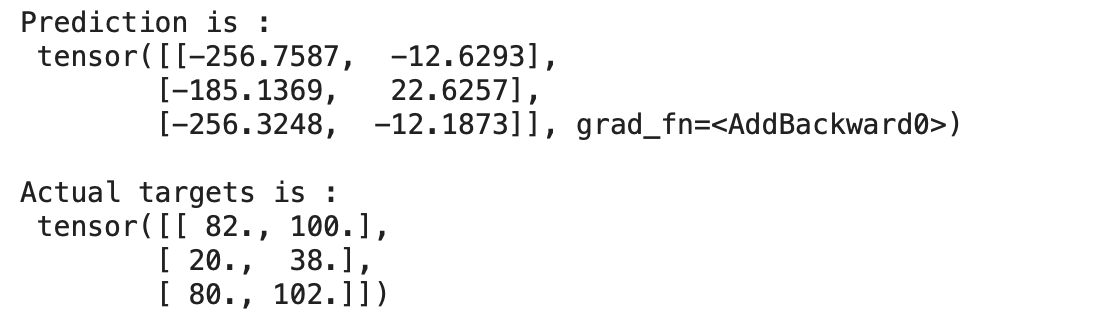
我們可以在上面看到我們的模型預測的值與實際目標相差很大，因為我們的模型是用隨機權重和偏差初始化的。

顯然，我們不能指望我們隨機初始化的模型表現良好。

損失函數

損失函數是衡量模型表現如何的指標。損失函數在更新超參數方面起著重要作用，因此產生的損失會更少。

回歸最廣泛使用的損失函數之一是均方誤差或L2 損失。

MSE 定義了實際值和預測值之間差異的平方平均值。MSE如下：

def?mse_loss(predictions,?targets):difference?=?predictions?-?targetsreturn?torch.sum(difference?*?difference)/?difference.numel()

.numel()方法返回張量中的元素數。

現在讓我們進行預測并計算未經訓練的模型的損失，

for?x,y?in?train_loader:preds?=?model(x)print("Prediction?is?:n",preds)print("nActual?targets?is?:n",y)print("nLoss?is:?",mse_loss(preds,?y))break

輸出：


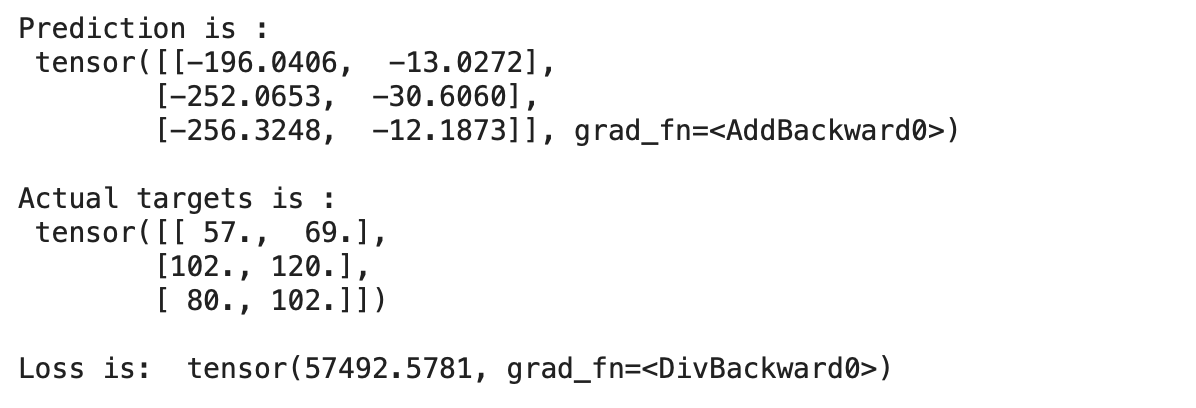
我們可以看到我們的預測與實際目標相差很大，這表明模型的損失很大。

因此，我們應該更新權重和偏差，以減少損失。這可以通過使用稱為梯度下降的優化算法來完成。

梯度下降

梯度下降是一種一階迭代優化算法，用于尋找可微函數的局部最小值。這個想法是在當前點的函數梯度（或近似梯度）的相反方向上重復步驟，因為這是最陡下降的方向。– 維基百科

梯度下降是一種優化算法，它計算損失函數的導數/梯度以更新權重并相應地減少損失或找到損失函數的最小值。

在 PyTorch 中實現梯度下降的步驟，

• 首先，計算損失函數

• 求關于自變量的損失梯度

• 更新權重和 bais

• 重復以上步驟

現在讓我們開始編碼并實現 50 個 時期的梯度下降，

epochs?=?50 for?i?in?range(epochs):#?Iterate?through?training?dataloaderfor?x,y?in?train_loader:#?Generate?Predictionpreds?=?model(x)#?Get?the?loss?and?perform?backpropagationloss?=?mse_loss(preds,?y)loss.backward()#?Let's?update?the?weightswith?torch.no_grad():w?-=?w.grad?*1e-6b?-=?b.grad?*?1e-6#?Set?the?gradients?to?zerow.grad.zero_()b.grad.zero_()print(f"Epoch?{i}/{epochs}:?Loss:?{loss}")

輸出：


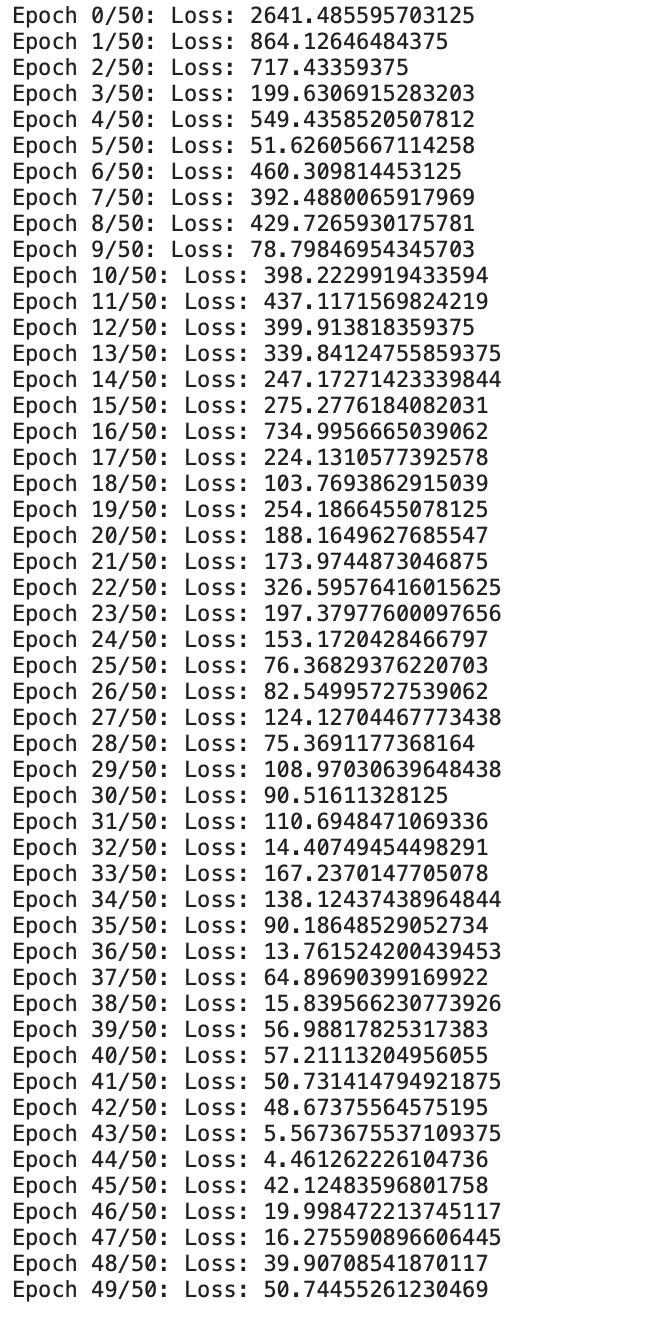
現在我們可以看到我們從頭開始定制的線性回歸模型正在訓練給定的數據。

我們可以看到損失一直在逐漸減少。現在讓我們檢查一下輸出，

for?x,y?in?train_loader:preds?=?model(x)print("Prediction?is?:n",preds)print("nActual?targets?is?:n",y)break

輸出：

我們可以看到預測幾乎接近實際目標。我們能夠通過訓練/更新線性回歸模型的權重和偏差來預測 50 個時期。

結論

這種在數據集每次迭代后通過我們基于損失的模型使用梯度下降更新權重/參數的過程定義了深度學習的基礎，它可以解決包括視覺、圖像、文本等在內的大量任務

往期精彩回顧適合初學者入門人工智能的路線及資料下載(圖文+視頻)機器學習入門系列下載中國大學慕課《機器學習》（黃海廣主講）機器學習及深度學習筆記等資料打印《統計學習方法》的代碼復現專輯 AI基礎下載機器學習交流qq群955171419，加入微信群請掃碼：

總結

以上是生活随笔為你收集整理的【深度学习】PyTorch 中的线性回归和梯度下降的全部內容，希望文章能夠幫你解決所遇到的問題。

如果覺得生活随笔網站內容還不錯，歡迎將生活随笔推薦給好友。