參考學習：Signal Generation and Preprocessing

本人只是為了了解信號處理的基礎知識而做的學習筆記，涉及深度可能不夠，有理解錯誤的地方請大膽指出，感激不盡

一、信號生成和預處理

(一)信號生成

從數據中去除噪聲、離群值和亂真內容。增強信號以對其可視化并發現模式。更改信號的采樣率，或者使不規則采樣信號或帶缺失數據信號的采樣率趨于恒定。為仿真和算法測試生成脈沖信號和 chirp 等合成信號。主要分為以下幾個步驟

1.創建波形

1.1周期波形Periodic Waveforms

sawtooth(T) 鋸齒或三角波

quare(T)函數產生一個2*pi為周期的方波

1.2 非周期波形Aperiodic Waveforms

1.3 掃頻波形Swept-Frequency Waveforms

1.4 脈沖序列Pulse Trains [Y=pulstran (t,d,

@func ,w,b)函數](https://blog.csdn.net/wwjra/article/details/7728892#commentBox) + 其中t為時間軸 + d為采樣間隔，可以是兩列，第一列對應偏移量，第二列對應增益量,說白了定義就是第一列定義產生每個波形的位置，第二列定義波形的高度 + w是每個波形的寬度 + b表示是每個波形高度對應X軸上下比例，0.5表示上下一樣大，0.8表示上部分高度和下部分高度成0.8的比例 + fun表示指定了脈沖串的形狀，包括： 高斯調制正弦信號：gauspuls 非周期的矩形信號：rectpuls 非周期的三角信號：tripuls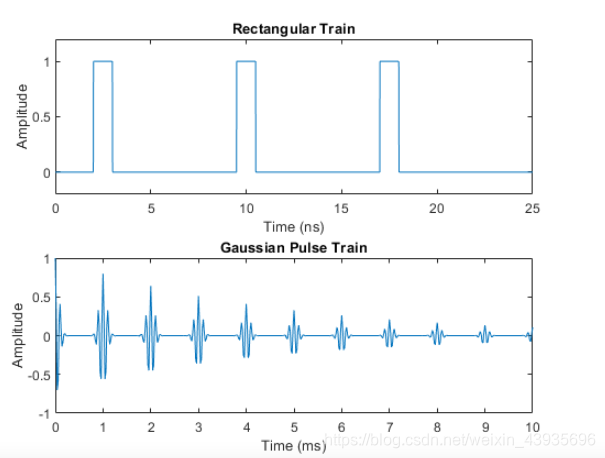 

(二)信號預處理

1. 平滑去噪

從信號中去除不需要的峰值、趨勢和離群值。使用 Savitzky-Golay 濾波器、移動平均值、移動中位數、線性回歸或二次回歸對信號進行平滑處理。

1.1 去峰值

1.2 離群值

filloutliers 檢測并替換數據中的離群值

isoutlier 查找數據中的離群值

1.3 去趨勢remove trend

信號的基線發生了偏移，有的是線性偏移，有的是非線性偏移，處理方式不一樣

線性的處理，使用函數detrend

dt_ecgl = detrend(ecgl);

非線性的，對信號進行低階多項式擬合并減去它

opol = 6;%多項式為6階

[p,s,mu] = polyfit(t,ecgnl,opol);

f_y = polyval(p,t,[],mu);

dt_ecgnl = ecgnl - f_y;

處理后

案例執行：openExample(‘signal/RemoveInstrumentDriftFromMeasurementsExample’)

2. 重采樣

重采樣分為上采樣和下采樣，下采樣時需要對信號進行抽取，上采樣時需要對信號進行插值

減少抽樣率以去掉過多數據的過程稱為信號的抽取(decimatim )”，增加抽樣率以增加數據的過程稱為信號的“插值(interpolation)。

resample 函數將序列的采樣率更改為與原始采樣率成一定比例的采樣率

2.1 重采樣的函數

應用帶重采樣的 FIR 濾波器

upfirdn

三次樣條插值

spline

抽取

decimate

插值

interp

其他一維插值

interp1

以新采樣率重采樣

resample

二、測量和特征提取

(一)測量和提取的因子

1. 描述性統計量

峰值

RMS 水平

峰間幅值

波峰因子

動態時間畸變

CUSUM 控制圖

編輯距離

2. 脈沖和轉換指標

上升時間

下降時間

壓擺率

過沖就

欠沖

穩定時間

脈沖寬度

占空比

3. 頻譜測量

通道功率

帶寬

均值頻率

中位數頻率

諧波失真

三、相關性和卷積

(一)目的

利用相關性和卷積函數，用于檢測信號相似性。確定周期性，找到隱藏在長數據記錄中的感興趣的信號，并測量信號之間的延遲以同步它們

(二)常見應用

在測量中找到信號

確定一個信號是否與一段較長的噪聲數據流相匹配。

對齊兩個簡單信號

學會使用互相關來對齊不同長度的信號。

將信號與不同開始時間對齊

同步不同傳感器在不同時刻采集的數據。

使用互相關性對齊信號

使用互相關性融合異步數據。

使用自相關求周期性

驗證含噪信號中是否存在周期，并確定其持續時間。

回波抵消

使用自相關來過濾語音記錄中的回聲

(三)互相關和自相關概念

1. 互相關

互相關函數是描述隨機信號x(t),y(t)在任意兩個不同時刻t1，t2的取值之間的相關程度

2. 自相關

自相關函數是描述隨機信號x(t)在任意兩個不同時刻t1，t2的取值之間的相關程度

(四)信號的卷積

1. 作用

提供一種方便的頻域處理方式

簡單的應用就是頻域濾波

2. 原理

輸出函數是輸入函數和系統函數的卷積

一個函數(如：單位響應)在另一個函數(如：輸入信號)上的加權疊加

對于線性時不變系統，如果知道該系統的單位響應，那么將單位響應和輸入信號求卷積，就相當于把輸入信號的各個時間點的單位響應 加權疊加，就直接得到了輸出信號。

四、數字和模擬濾波器

(一)數字濾波器設計

1. IIR濾波器

Finite impulse response filters， 有限脈沖響應濾波

1.1 與 FIR 濾波器的比較

優點： 要滿足同一組設定，它的濾波器階數通常遠遠低于 FIR 濾波器

1.2 IIR分類

Butterworth 濾波器

Chebyshev I 類濾波器

Chebyshev II 類濾波器

橢圓濾波器

2. FIR濾波器

Infinite impulse response filters，無限脈沖響應濾波器

2.1 與IIR濾波器比較

優點：

它們可以具有精確的線性相位。

它們始終穩定。

設計方法通常是線性的。

它們可以在硬件中高效實現。

濾波器啟動瞬態具有有限持續時間。

2.2 濾波器設計方法

加窗

對指定的矩形濾波器的截斷傅里葉逆變換應用加窗

多頻帶(包含過渡帶)

對頻率范圍的子帶使用等波紋或最小二乘方法

約束最小二乘

根據最大誤差約束，在整個頻率范圍內最小化平方積分誤差

任意響應

任意響應，包括非線性相位和復濾波器

升余弦

具有平滑正弦轉換的低通響應

(二)數字濾波器分析(未學習)

(三)數字濾波(未學習)

(四)多采樣率信號處理(未學習)

(五)模擬濾波器(未學習)

五、變換(未學習)

六、頻譜分析(未學習)

七、時頻分析(未學習)

八、信號建模(未學習)

九、振動分析(未學習)

十、深度學習處理信號

(一)需要做的任務

信號標注

特征工程

數據集生成

(二)信號處理用到的函數

1. 標注函數

labeledSignalSet

創建標記信號集

signalLabelDefinition

創建信號標簽定義

2. 數據存儲函數

signalDatastore 用于收集信號的數據存儲

3. 特征提取函數

findchangepts 發現信號的突變

findpeaks 找到局部極大值

findsignal 利用相似性搜索尋找信號定位

fsst 傅里葉同步壓縮變換

instfreq 瞬時頻率估計

pentropy 信號的光譜熵

periodogram 周期圖功率譜密度估計

pkurtosis 信號或譜圖的光譜峰度

powerbw 功率帶寬

pspectrum 在頻域和時頻域分析信號

pwelch 韋爾奇功率譜密度估計

(三)信號處理的APP

Signal Analyzer

可視化并比較多個信號和頻譜

Signal Labeler

標記信號屬性，區域和興趣點

總結

以上是生活随笔為你收集整理的机器学习处理信号分离_[学习笔记]使用机器学习和深度学习处理信号基础知识...的全部內容，希望文章能夠幫你解決所遇到的問題。

如果覺得生活随笔網站內容還不錯，歡迎將生活随笔推薦給好友。